BigO
알고리즘의 증가 추세로 표시하는 시간 복잡도 표기 방법
2n^2도, 3n^2도 O(n2)로 같다. loop를 한번 쓰면 최악의 경우 모든 계산을 한다. 즉 n번을 계산하게 되므로 루프 시 n*n⇒ n^2가 된다.
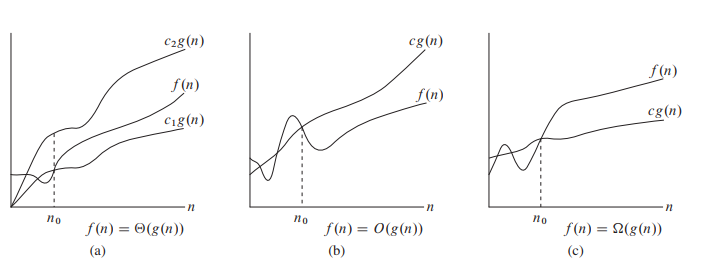
Big O -upper bound Big Omega - lower bound Big Theta - Tight bound
| 어떤 경우? | 최악의 경우 | 최선의 경우 | |
| ≤ | ≥ | == | |
| 알고리즘의 성장 속도 | 특정 값보다 작거나 같음 | 특정 값보다 크거나 같음 | 특정 값과 같 |
| 무엇을 표시? | 알고리즘의 상한을 표시 | 알고리즘의 하한을 표시 | 상한과 하한의 The bounding of function 을 표시 |
| asymptotic bound(점근적 결합) | asymptotic upper bound를 제공 | asymptotic lower bound를 제공 | The exact asymptotic behavior is done by this theta notation. |
| 정의 | 알고리즘의 가장 최악의 성능에 대한 상한선을 정의(가장 많이 시간을 잡아먹는 경우를 말함) | 알고리즘의 가장 최선의 성능에 대한 하한선을 정의(가장 적게 시간을 쓰는 경우를 말함) | 알고리즘이 가질 수 있는 가장 최악의 경우들 중 최선의 선택지를 가장 tight한 bound라고 정의함 |
| 수학적 접 | Big Oh is 0 <= f(n) <= Cg(n) for all n >= n0 | Big Omega is 0 <= Cg(n) <= f(n) for all n >= n0 | Big Theta is 0 <= C2g(n) <= f(n) <= C1g(n) for n >= n0 |
47p
연산과 알고리즘
시간복잡도는 알고리즘을 수행하는데 연산들이 몇 번 이루어지는지를 숫자로 표시한다. 여기서 연산은 산술/대입/비교/이동 을 뜻하는데, 이런 연산operation은 딱 정해진 횟수(constant)가 아니라 입력한 데이터의 갯수에 따라 달라진다. 보통 이런 입력된 데이터를 n이라 표기한다.
시간복잡도
- 차후 추가
공간복잡도
- 차후 추가
reference
https://madplay.github.io/post/time-complexity-space-complexity
https://www.geeksforgeeks.org/difference-between-big-oh-big-omega-and-big-theta/
'공부기록 > Algorithm' 카테고리의 다른 글
| [TIL][TUE] 병합정렬/퀵정렬 (1) | 2023.10.17 |
|---|---|
| [TIL][Mon] 정렬 (2) | 2023.10.16 |
| [TIL][W1/Sun] 소수찾기 (0) | 2023.10.16 |
| [TIL][W1/Sun] 반복 (0) | 2023.10.15 |
| [TIL][W1/Sat] 배열/문자열 (0) | 2023.10.14 |
